Als je aan een kring meet zul je altijd die kring beinvloeden. Wat je ook doet. Daarom is er een belaste en een onbelaste Q. Bij resonantie geeft in theorie de condensator al zijn energie aan de spoel en de spoel weer aan de condensator. Alleen bevat elk component verliesgevende onderdelen. Bij de condensator bv de ESR en de verliezen in de pootjes, soldeerverbindingen. Bij de spoel de ohmse weerstand, de skin effect verliezen maar ook de omgeving. Dingen zoals eddy currents, proximity effecten, stralingsverlies. Maar ook de energie die wij er uit halen simpelweg om het te meten. De kring werkt als antenne en de stralingsweerstand stijgt met de vierde macht van de frequentie.
Dit gaat niet over hoe je de Q berekent aan de hand van de metingen, dat staat in mijn VNA tutorials uitgebreid beschreven maar om het maken van een juiste meetopstelling en welke signalen je kan verwachten. Dit is gedaan met een VNA maar het kan ook met een SA en TG. Een meting valt en staat met de opstelling en soms zit je naar dingen te kijken die er alleen zijn omdat je ze zelf hebt veroorzaakt. bv een resonantie in een DUT houder.
De verschillen in resonantie
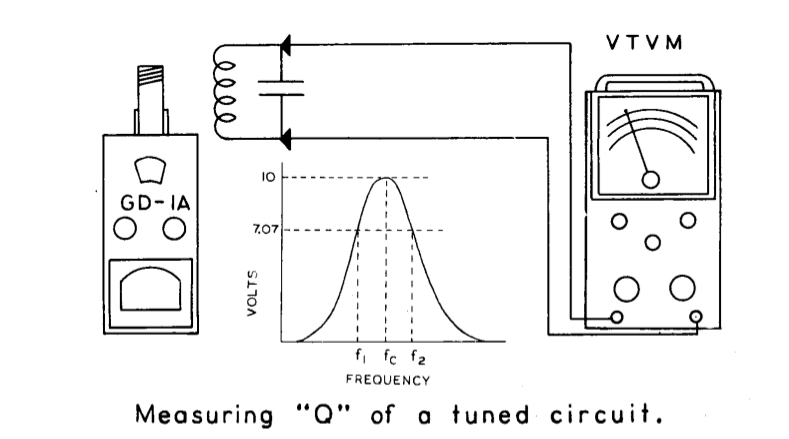
Nu kun je die kring direct aankoppelen op de VNA. Dan belast je hem aan beide kanten met 50 ohm. Of tussen twee EH probes ofwel koppelspoelen hangen. Een derde methode wordt onderaan nog besproken.
Alle metingen tegelijk in het scherm
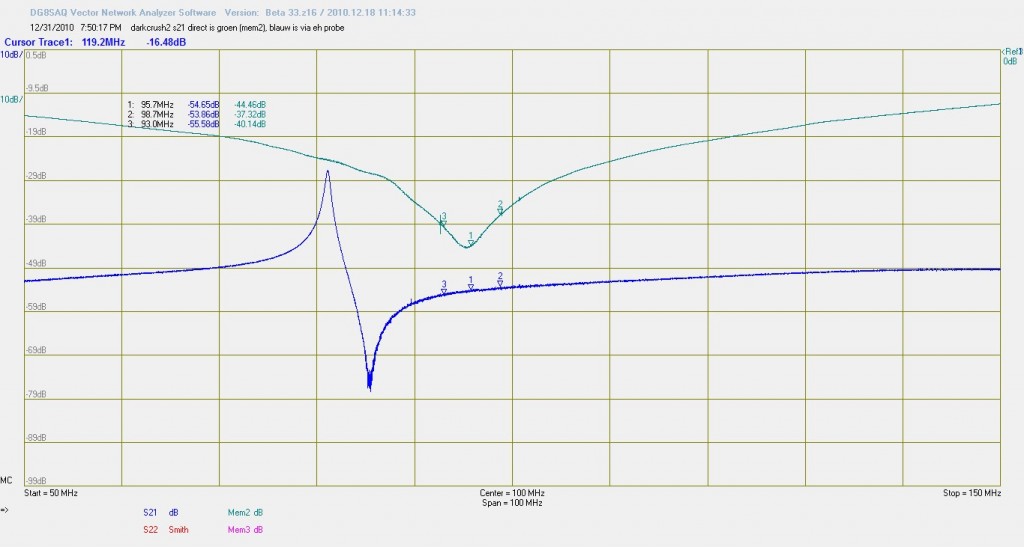
Je ziet dat de resonantie van de kring een paar MHz lager ligt bij de methode middels in- en uit-koppelspoelen.
De groene trace, mem1 is een S21 directe inspanning. Door de belasting neemt de Q af en verschuift de resonantie. De kring vormt een hoge weerstand en op de resonantie frequentie daarom een dip.
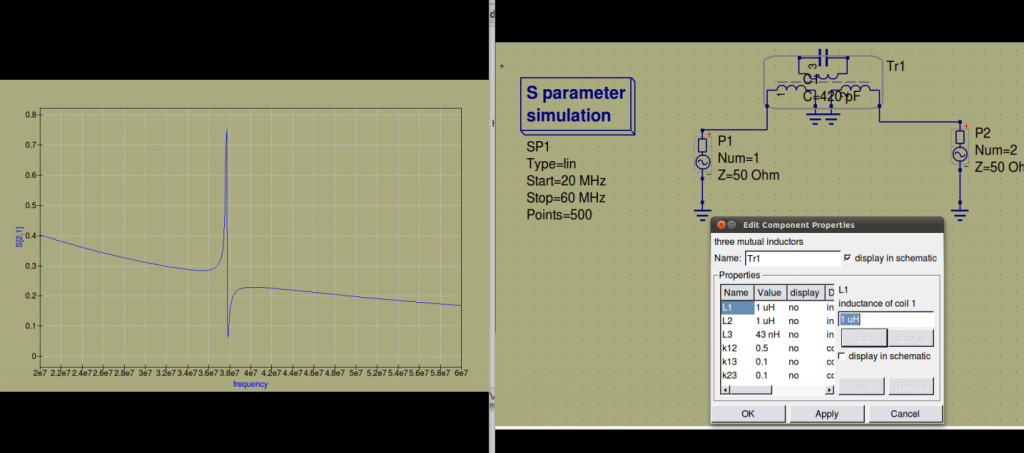
De blauwe S21 is een meting met twee H probes die 3 cm naast elkaar voor de kring worden gehouden. (als een soort brilletje zeg maar) Je ziet een dip en dan een piek. Heel opvallend is dat die hoog/laag reactie heel veel voorkomt bij meting middels in en uitkoppelen. De ene keer eerst een dip maar ook eerst een berg en dan een dip. de oorzaak komt door te sterke onderlinge koppeling van de in en uitkoppelspoel. Zie deze simulatie:
Vast gekoppelde meetspoelen
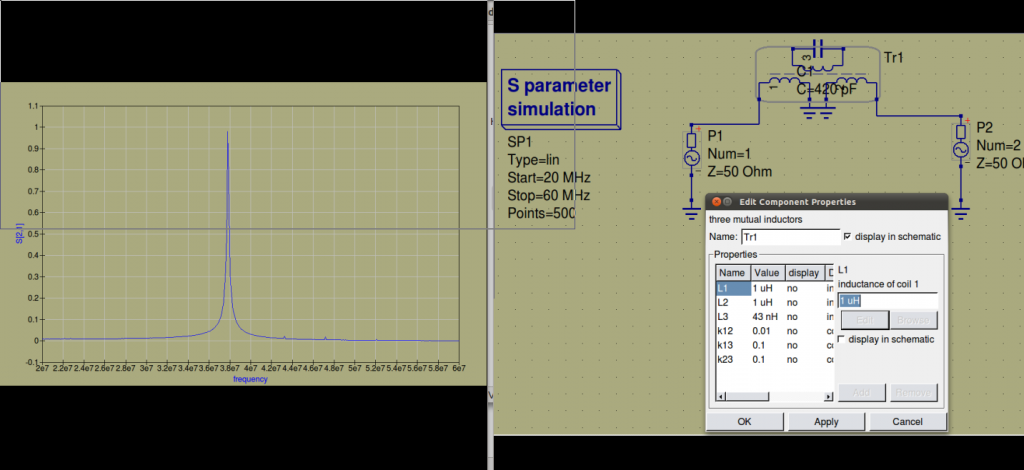
Bij een hoge K tussen de twee uitkoppelspoelen of H-probes onderling krijg je deze dubbelresonantie. Verlagen we K een stuk, dus de spoelen verder uit elkaar dan wordt het zoals het hoort:
Losse koppeling
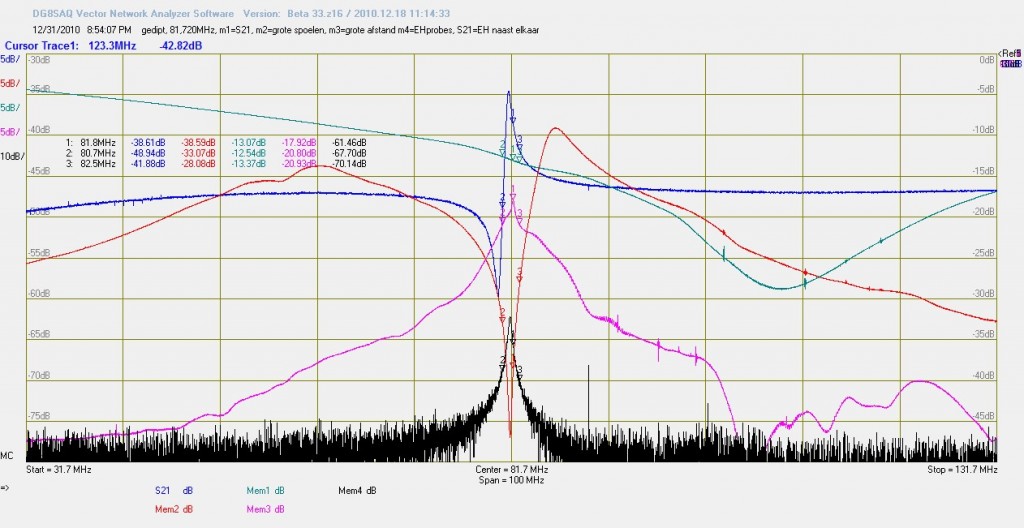
In het boek van Nussbaum over metingen met een netwerktester worden deze methode beschreven. Daarbij toont hij traces zoals mem3, de roze. Hierbij heb ik de grote spoelen op een grotere afstand gehouden. Ook mem4, de zwarte trace is op afstand, dit waren de kleine EH probes. Wat je ziet is de energie circulatie in de spoel. Door de afstand gaat de rest verloren maar de spoel zendt als het ware op zijn resonantie frequentie uit.
Die golfbeweging (blauw) komt door onderlinge koppeling van de spoelen. Zoals je aan de fase op de HP hieronder ziet (de metingen met fase op de digitale vna lieten het zelfde zien) is de bult een fasesprong (misschien vanwege de afstand tussen de probes een verzwakte resonantie) maar de dip een echte resonantie. Die wordt veroorzaakt door de twee koppelspoelen . De twee koppelspoelen zonder DUT laten geen resonanties zien.
HP VNA, 10MHz span. Het " pannetje" is de fase.
Hier zie je ook de spoel in de DUT houder op zijn zijkant.
Een paar EH probes. De zwarte klont is een ferriekern
S21 direct
Dat zie je hier bij de directe meting. De fase verspringt 180 graden.
De meetopstelling met een sweep van 1 tot 110MHz
Kortom, het valt niet mee om aan resonantiekringen te meten. Waar zit hij nu echt. Volgens een ouderwetse maar betrouwbare methode zat hij op 81,72MHz. Hoe ik dat heb gemeten. Heel simpel, met een heel goede dipmeter op ongeveer 50 cm afstand en die frequentie weer gemeten met een counter.
Volgens Nussbaum moet je voor Q meten bij hoge Q kringen, de kring vrij ophangen en de meetspoelen op 10cm van de kring hangen. De Q is dan √(L/C).Rs waarbij Rs de verliesweerstand van de kring is.
Ook met een griddipper kan je aan spoelen meten
Update 19 januari:
Wat met een griddipper kan zou ook met een VNA moeten kunnen.
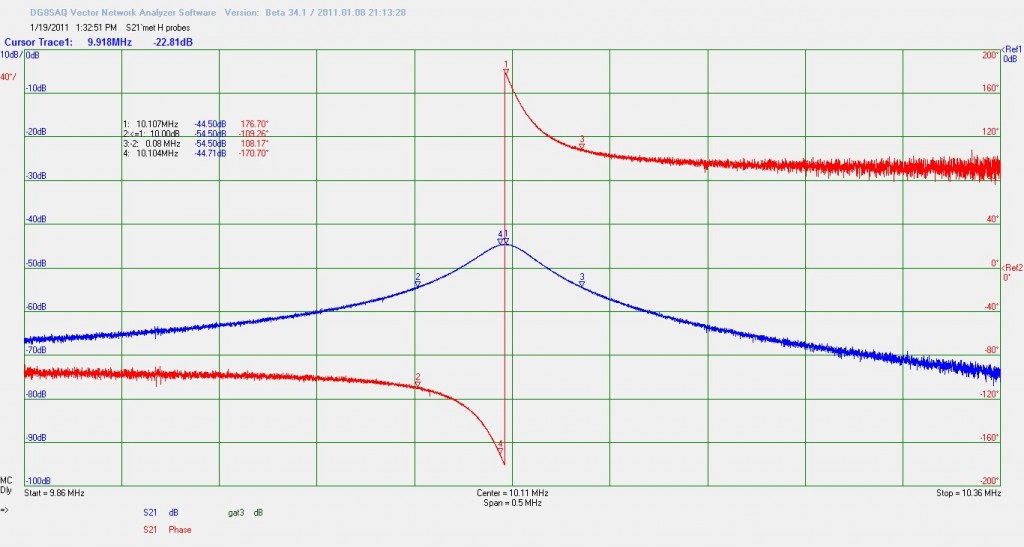
Dit keer een andere spoel op een varco, gewoon even een standaard opstelling. Eerst als referentie de methode met de twee H-probes.
S21 met twee H-probes
fc= 10.106.718,3 Hz, f1= 10.061.607,8 Hz, f2= 10.145.533,0 Hz , de bandbreedte is 83.925,2 Hz. De fasesprong is over 217,42 graden, Q kring 120,4
Daarna de VNA als griddipper:
S11 VNA als griddipper
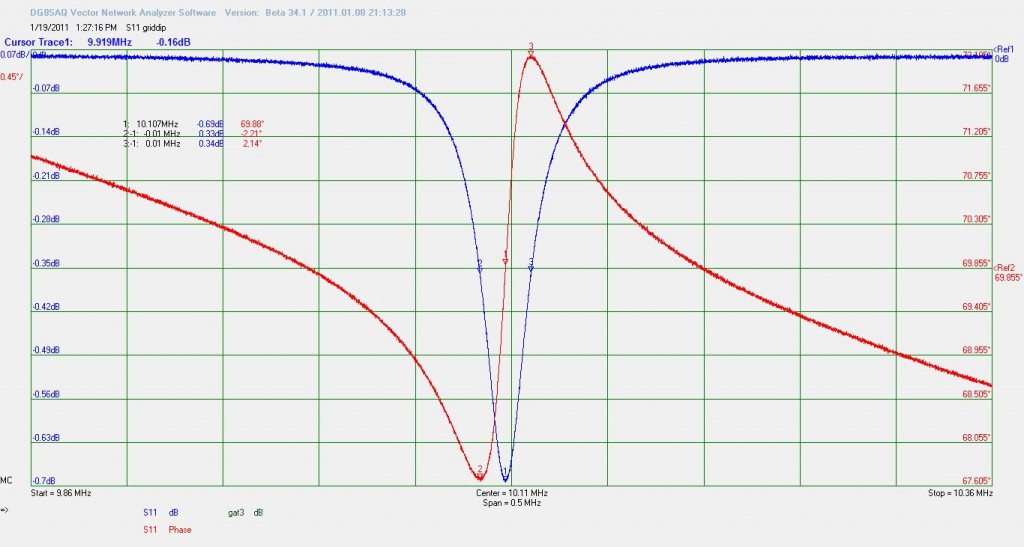
De VNA is hiervoor voorzien van een oppikspoel en deze is zover mogelijk van de kring afgehouden totdat de bandbreedte niet verder versmalde maar er in ieder geval nog een bruikbare dip te zien was bij een S11 reflectie meting. (je praat over een hele kleine koppeling, de dip geeft een Rl van ongeveer 0,7dB dus dat is heel weinig). Ik neem hier de dip op de top en de bodem van de fasesprong en de lengte van de fasesprong als norm voor de bandbreedte.
fc= 10.106.712,3 bij 69,883 graden dat is precies de zelfde frequentie, een goed teken. f1= 10.093.437,3 / 67,672graden en f2= 10.119.937,6 / 72,025 graden. Dat is een BW van 26.500,3Hz en 4,353 graden. Q=381,38
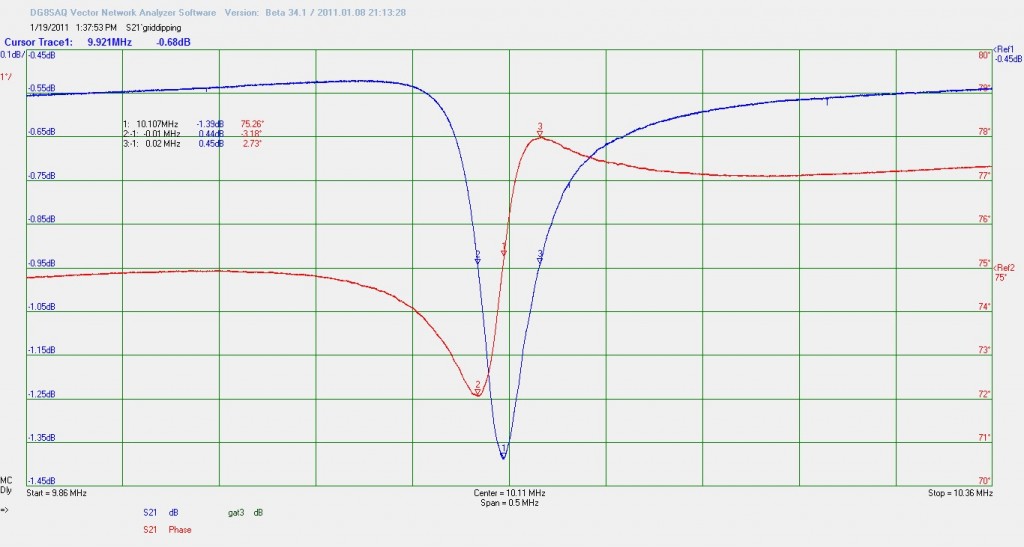
De derde methode is een T stuk tussen de beide poorten met daarop een oppikspoel.
S21 griddipper
Bij het meten heb ik misschien het circuit per ongeluk wat verplaatst, dat vandaar misschien de iets andere frequentie maar ook de bandbreedte is groter dus het kan ook de invloed van de meting zijn.
fc= 10.107.030,9 bij 75,263 graden, f1= 10,093.514,4 bij 72,084 graden en f2= 10.125.709,9 bij 77,988 graden. Dat levert een BW van 32.295,5Hz op over 5,904 graden. en een Q van 312,9
De spoel zelf was op 10,1MHz 2,87 uH en ongeveer 160mΩ . Door dat hij signaal oppikt varieerde de Q en de R-. Dit varierde van 1000 tot 8000. Bij grove afscherming was de Q ongeveer 1175 en verliep nog maar weinig.
De varco was 84,84 pF/ R-1 ohm en D 0,00558. Dat levert 10,195 MHz op. Het verschil zit hem in de paracitaire effecten tussen metalen varcokast met banaan/bnc klem en spoel die beide los tov gemeten zijn.
De BW van de kring zou onbelast dus 8,67KHz zijn bij een ideale condensator. Echter de condensator en connector en aansluiting er naar toe zijn ook niet ideaal dus dat verklaart de grotere bandbreedte. Er zit dus ergens tussen 500 en 1000mΩ in die tak en dat verlaagd de Q van de kring tussen 30 en 60K. Het is dus best de moeite draadjes en verbindingen te optimaliseren.